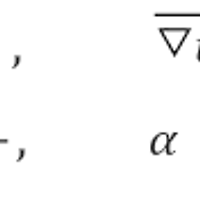본문 바로가기
OpenFOAM/배경이론 간단정리

[OpenFOAM 배경이론 간단정리] 압력-속도 연성

하루생각+ 2016. 4. 12. 22:24


작성일 : 2015년 10월  17일
번역일 : 2016년    4월  12일


크롬 브라우저로 보시는 것을 권장해 드립니다.


 ------ OpenFOAM 소스코드 파해치기 시리즈 ------

OpenFOAM 소스코드 파해치기 목차로 이동

 ------------------------------------------------------------

 ----- OpenFOAM 소스코드를 다루는 문법 기본 -----

OpenFOAM 소스코드를 다루는 문법 기본으로 이동

 ------------------------------------------------------------



 


  3. 압력-속도 연성


3.1  압력방정식

     운동방정식을 반이산화하면, 다음과 같은 식으로 표현할 수 있다.
(식 41)


여기서, A 는 계수로, 아래첨자 P 는 주목하는 셀을, N 은 주목하는 셀의 옆에 있는 셀을 나타낸다.

     OpenFOAM 에서는 우변을 없애고

(식 42)


으로, 다음과 같이 표현한다.

(식 43)


따라서 운동방정식은

(식 44)


속도는 다음과 같이 적을 수 있다.

(식 45)


     이것을 연속의식 (식 1) 에 대입하면,

(식 46)


따라서,

(식 47)


정상상태인 경우, 우변의 시간미분항은 생략할 수 있다. 비압축성유체의 경우,

(식 48)


     위의 압력방정식을 풀어 얻어낸 압력으로부터, 식 (45)에 의해 새로운 속도를 구해낸다.



3.2  SIMPLE 법
     OpenFOAM의 정상해석솔버에서는, 압력-속도연성방법으로 SIMPLE법을 사용하고 있다. 일반적인 Patankar 에 의한 형식과는 조금 다르며, 상당히 단순하다. 계산순서는 아래와 같다.
1. 운동량방정식 (44) 를 풀어, 속도를 구한다.
2. 압력방정식 (47) 또는 (48) 을 풀어, 압력을 구한다.
3. 식 (45) 를 이용해 속도를 갱신한다.

이상의 순서를 통해 Residual이 작아질때까지 반복계산을 수행한다.



3.3  SIMPLEC 법
     OpenFOAM의 일부 솔버에서는 SIMPLEC 법을 사용하고 있다. SIMPLEC 법의 계산에는  Σ A_N 이 필요하나, OpenFOAM 에서는 방정식 H1 함수로 얻어낸다. 방정식은 조금 다르지만, 계산순서는 SIMPLE법과 동일하다.



3.4  PISO 법
     OpenFOAM의 비정상솔버의 일부는 PISO 법을 사용한다. OpenFOAM의 형식에서는, 계산순서가 아래와 같다.
1. 운동량방정식 (44) 를 풀어, 속도를 구한다.
2. 압력방정식 (47) 또는 (48)을 풀어, 압력을 구한다.
3. 식 (45) 에 의해 속도를 갱신한다.
4. 이상의 압력 계산과 속도 갱신을 지정회수만큼 반복한다 (통상 2회).
위의 순서를 필요한 시간스텝만큼 반복계산한다.



3.5  PIMPLE 법
     OpenFOAM의 비정상 솔버에서는 PISO 법과 SIMPLE 법을 조합한 "PIMPLE 법" 을 사용한다. 이것은 시간 스텝의 사이에 SIMPLE 법의 루프를 넣은 것에 해당한다.
1. 운동량방정식 (44) 를 풀어, 속도를 구한다.
2. 압력방정식 (47) 또는 (48) 을 풀어, 압력을 구한다.
3. 식 (45) 를 이용해 속도를 갱신한다.
4. 위의 압력 계산과 속도의 갱신을 지정회수만큼 반복한다 (통상 2회).
5. 이상의 순서를 Residual 이 작아질때까지 반복계산한다.
이상의 순서를 필요한 시간 스텝만큼 반복계산한다.



3.6  압력진동의 회피
     속도와 압력의 값을 같은 위치에서 가지는 코로케이트 격자(co-locate gird)에서는, 압력징동이 발생한다는 것이 알려져 있다. 이것을 피하기 위해서는, 속도와 압력의 값을 가지는 위치를 다르게 설정한 스테거 격자(staggered grid)를 이용하는 방법이 있으나, 코로케이트 격자를 이용하는 방법으로 Rhie and Chow 에 의한 방법이 있다. OpenFOAM 에서는, 코로케이트 격자를 사용하므로 후자의 방법을 채용하고 있다.
     압력진동은, 압력구배의 이산화 방법에서 발생한다. 셀의 경계에 보간한 속도 u_f 는, 식 (45) 를 통해 아래와 같은 식으로 표현된다.
(식 49)


     Rhie and Chow 의 방법에서는, 위 식을 다음과 같이 수정한다.

(식 50)


이것에 의해 새로운 항이 추가된 것이 되나, 이 항이 압력징동을 제어하는 동작을 수행한다.

     OpenFOAM에서는, 위의 식을 유속 phi 로 표현하고 있다. 여기서 유속 phi 는, 셀 경계면의 면적벡터를 S 로하고, 압축성유체솔버에서는 phi = rho u * S, 비압축성유체솔버에서는 phi = u * S 이다. OpenFOAM 의 솔버에서는, 운동량방정식의 구축에 phi 가 사용되거나, 속도의 갱신과는 별개로 phi 가 갱신되고 있거나 하는 것은 이 Rhie and Chow 에 의한 보간법을 사용하고 있기 때문이다.



3.7  유체 flux 의 수정
     OpenFOAM 에서는, 유체플럭스 phi 를 수정하는 동작이 이루어지고 있다. 수정에는 2가지가 있으며, 비정상해석에 의한 ddtPhiCorr 와, 질량의 유입과 배출의 밸런스를 조정하는 adjustPhi 가 있다.
     ddtPhiCorr 는, 이전 단계에서의 속도 u 에서 계산되는 유체 flux와 이전 단계의 유체 flux인 phi (이것은 이전이전 단계에서 속도로부터 계산되었다)의 차이를 보정하는 역할을 한다. 비압축성유체솔버의 경우, 다음과 같은 계산이 수행된다.
(식 51)


여기서 u_0 는 이전단계의 속도, phi_0 는 이전단계의 유체 flux 에 해당한다. ddtPhiCorr 의 본체는, EulerDdtScheme 등 시간미분스킴 속의 fvcDdtPhiCorr 로 정의되어있으며, 위 식의 우변의 괄호 안의 내용이 ddtScheme 안에서 fvcDdtPhiCorrCoeff 로 정의되어 있다.

     외 이런 방식으로 되어 있는지 다음과 같이 유추해 볼 수 있다. 계산상, 연속의 식을 엄밀히 만족할 수 없으며, 오차가 발생하게 된다. 이것을 고려해보자. 먼저, 비압축성유체일때, 운동방정식은 반이산화식에서 시간미분의 항은 다음과 같이 된다.

(식 52)


따라서,

(식 53)


이산화하면, 연속의 식에서 우변의 2번째 항이 사라지게 된다. 하지만, 계산상의 오차로 인해 0이 되지 않으므로, 이 항을 남겨둔다. 양의 값으로 계산하는 가정으로, backwind 스킴으로 이산화하면,

(식 54)


여기서 u_00은 전전 단계에서의 속도를 의미한다. OpenFOAM에서는, Divergence의 계산에 유체 flux 를 사용하므로, 유체 flux의 형태로 표현하면,

(식 55)


이것으로 ddtPhiCorr 에서 계수를 제외한 항을 얻을 수 있다. ddtPhiCorr의 계수는 물리적인 항이 아닌 계산상의 안정화를 위한 항으로 생각된다. 즉, phi_0 - u_0*S 가 phi_0 에 비해 작을때만 보정되도록 하는 작용을 할 것이다 ( 식 (44)의 A와 H 는 시간미분항에서 유래하는 항을 포함하고 있을 것이며, 위에서 기술한 보정을 추가하면, 시간미분항을 2중으로 고려하게 된다는 것은 의아스럽다.)

     adjustPhi 에서는, 질량의 유출입의 조정을 수행한다. 단순한 흐름에서는, 유입질량유량 dot(m_in) 과 유출질량유량 dot(m_out)이 서로 평행상태이지만, 경우에 따라서 평행상태가 아니며, 질량보존을 위해 추가적인 질량유입을 고쳐한다. 이것을 dot(m_add) 라고 한다면,

(식 56)


이어야 한다. 실제로는 경계조건 때문에(?) 이것이 잘 맞지 않고, 다음과 같은 형태가 된다.

(식 57)


여기서,

(식 58)


adjustPHi 에서는, dot(m_add) 에 해당하는 면의 유체 flux 에 alpha 를 곱해 조정한다.



저작자표시 비영리 변경금지

'OpenFOAM > 배경이론 간단정리' 카테고리의 다른 글

[OpenFOAM 배경이론 간단정리] 경계조건  (0) 2016.05.11
[OpenFOAM 배경이론 간단정리] 유한체적법에 의한 이산화  (0) 2016.04.11
[OpenFOAM 배경이론 간단정리] 열유체의 구배방정식  (0) 2016.04.08
[OpenFOAM 배경이론 간단정리] 시리즈 목차  (4) 2016.04.05

'OpenFOAM/배경이론 간단정리' Related Articles

티스토리툴바